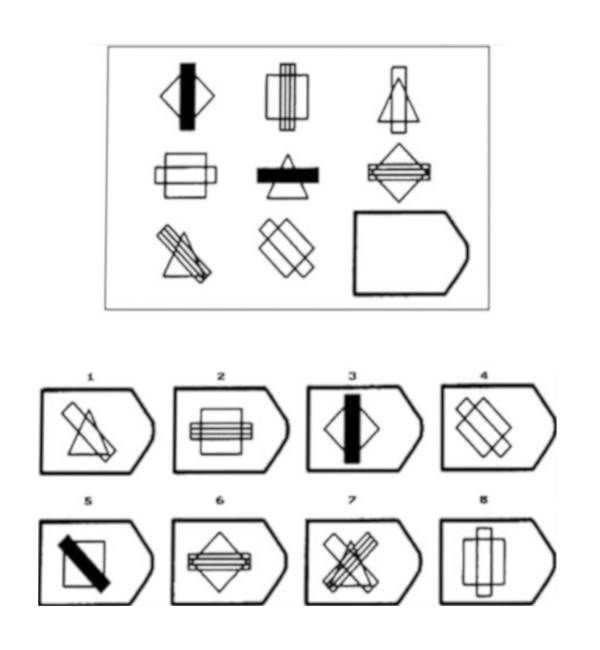
A common goal of AI is to create a human-like intelligence. It's hard to judge how human-like an AI agent is but one way we can measure that is by having an AI agent take the same intelligence tests that humans take. If an AI holds a human-like intelligence, it should be able to compete with human scores on these tests. A good example of one of those intelligence tests would be Raven's Progressive Matrices. As you can see in the image above, these are visual analogy problems where a matrix of figures is presented with the last figure omitted. The test-taker is then prompted to select the answer choice which logically completes the matrix.

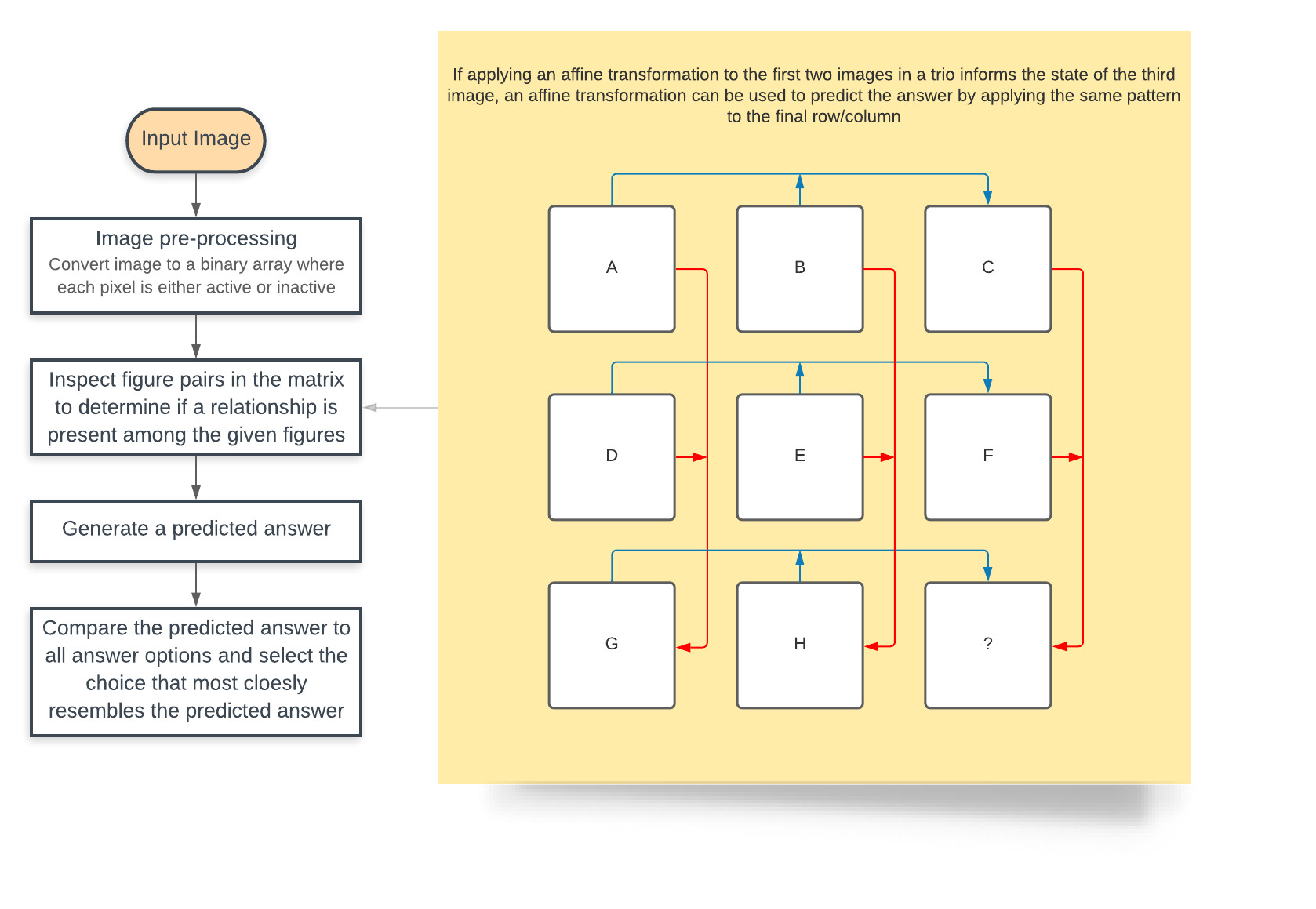
While machine learning is often used to develop agents, there is not always going to be enough training data available. For this project, I attempted to create an agent using Knowledge-Based practices. This posed an interesting challenge because I had to consider the way a human might solve these problems and attempt to implement that in code. The first approach my agent uses to solve these puzzles is testing for affine transformations. For those unfamiliar, an affine transformation is one that preserves lines and parallelism, but not necessarily distances and angles. So basically, this includes transformations such as scaling, rotating, mirroring, and panning. The agent will attempt to apply a variety of affine transformations to the first two images in each row and column. If the first two images are found to be related by an affine transformation, the agent will then check if the affine transformation applies further to the third image (If A -> B where '->' represents an affine transformation, then check if B -> C). If that is the case, then the first two images in the final row/column can be used to predict an answer (G -> H -> ?). This process is illustrated by the diagram below:



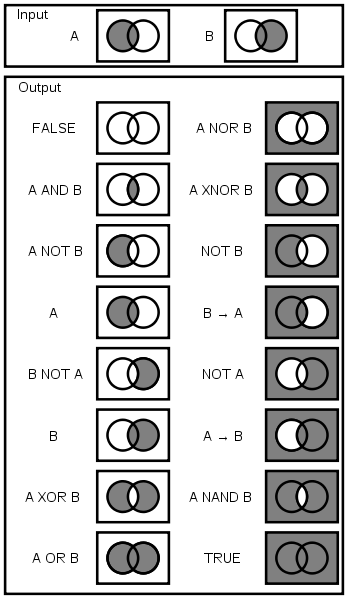
Not all problems will be solvable by affine transformations though. Some problems are solved by using logic gate combinations of images. This solution method works like above, except two images are required to perform a logic gate operation. This means that the agent tests if A|B -> C (where | represents the logic operation used) instead of testing if A -> B -> C. Below are some examples of the ways A and B can be combined using logic gates.



In addition to these two methods, my agent will count the number of pixels to determine if there is a constant change rate or a ratio that will inform the agent how many pixels it should expect in the answer. This is prone to error so as an additional helper, the agent also uses a flood-fill algorithm to count the number of shapes in each figure. Between the count of pixels and count of shapes, the agent can generally make reasonable guesses when the first two methods discussed fail.

I've talked about how the agent creates a predicted answer, but once it has a prediction, how does it know which answer choice matches that prediction? It would be easy to do a simple array comparison to see if the prediction equals each answer choice, but the data is never that perfect. Shapes and pixels inside each figure will vary slightly. The problems are created for humans who won't notice slight shifts or distortions, so the agent needs a way to figure out if two similar images are meant to be the same.

The similarity between two images can be calculated like so: $\text{similarity}(A\text{,}B)=\frac{f(A\cap B)}{f(A\cup B)}$
Using this, the agent calculates the similarity between its predicted answer and each answer choice. If any answer choice falls within a certain threshold, that answer choice is selected and the confidence of that answer choice is informed by the similarity percent. This allows an answer to be overwritten if a more confident answer is discovered later.

Lastly, just like any human, if the agent can't determine an answer, it takes a random guess.

Results

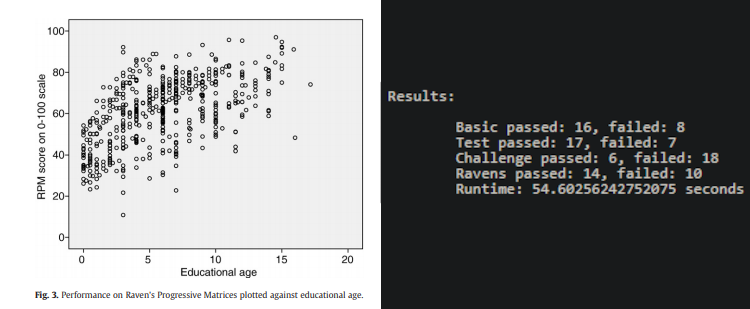
The chart on the left shows human performance on Raven's Progressive Matrices problems. A postive trend can be seen where performance improves with educational age. My agent correctly answered 53/96 problems resulting in an accuracy of ~55%. The overall mean of the data is 61.88 with a standard deviation of 15.97. This places my agent's results within less than half a standard deviation from the mean. While the agent's results are not spectacular, it does demonstrate that Knowledge-Based practices can produce an AI agent that is able to compete with human test-takers on a test designed to measure human intelligence.